|
Учебные материалы по физической химии
Реальные газы
2.4.Реальное статистическое описание
реальных газов
Точный теоретический расчет статистической
суммы газов или жидкостей с произвольным
гамильтонианом (2.6) - задача, которая лежит далеко
за пределами возможностей современной
статистической физики. Тем не менее, можно
сделать ряд разумных и достаточно хороших
приближений, которые позволяют оценить
статистическую сумму (2.1) и конфигурационный
интеграл (2.8) для реальных газов, состоящих из
валентно насыщенных молекул.
Главное из этих приближений состоит в том, что
общая потенциальная энергия взаимодействия
частиц может быть представлена в виде суммы парных
потенциалов, каждый из которых зависит только
от расстояния между двумя частицами rij =
|qi–qj|:
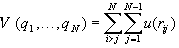 . (2.16) . (2.16)
Это приближение позволяет дать обоснование
закону соответственных состояний (см. § 1.5). Не
проводя конкретный расчет статистической суммы,
можно показать, что если все реальные газы
описываются парным потенциалом одного и того же
вида с двумя параметрами, то они подчиняются
одному и тому же уравнению состояния в
приведенных переменных.
2.4.1. Вывод закона соответственных
состояний
Предположим, что парный потенциал для всех
газов имеет вид
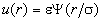 , (2.17) , (2.17)
где Y - универсальная функция для всех газов, а
параметры  и и  описывают конкретный
газ. Введем приведенные (безразмерные)
переменные описывают конкретный
газ. Введем приведенные (безразмерные)
переменные
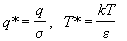
и вычислим в этих переменных конфигурационный
интеграл с учетом парного приближения (2.16)
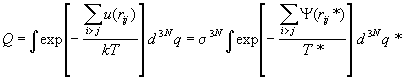 . .
Последний интеграл в этой формуле (обозначим
его Q*) - это безразмерный приведенный
конфигурационный интеграл; он одинаков для всех
газов. Если ввести приведенные давление и объем
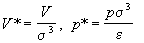 , ,
то приведенное давление выражается через
другие приведенные переменные универсальным
образом:
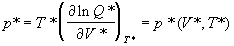 . (2.18) . (2.18)
Таким образом, данный вывод позволяет
сформулировать два условия выполнимости закона
соответственных состояний:
а) парный потенциал (2.17) должен быть
универсальным;
б) универсальный потенциал должен содержать
ровно два параметра.
2.4.2. Связь второго вириального
коэффициента с парным потенциалом
Для того, чтобы рассчитать конфигурационный
интеграл с потенциалом (2.16) в явном виде,
необходимо сделать еще несколько допущений
относительно парного потенциала. В частности,
для сходимости некоторых интегралов необходимо,
чтобы парный потенциал при больших расстояниях
стремился к нулю быстрее, чем r-3.
Фактически это означает, что существует
некоторая конечная область действия
межмолекулярного потенциала, за пределами
которой потенциал можно считать равным 0. Это -
довольно мягкое требование, которое
удовлетворяется для большинства реальных газов.
При подстановке аддитивного потенциала (2.16) в
конфигурационный интеграл экспонента под знаком
интеграла превращается в произведение,
содержащее N (N–1)/2 сомножителей:
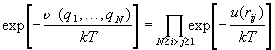 . (2.19) . (2.19)
При больших r каждый сомножитель стремится
к 1, поэтому довольно удобно выделить единицу из
экспоненты и определить функцию Майера следующим
образом:
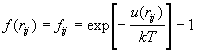 . (2.20) . (2.20)
При малых r потенциал стремится к
бесконечности, а функция Майера к –1; при больших r
и потенциал, и функция Майера довольно быстро
стремятся к нулю. На рис. 2.2 и в табл. 2.1 приведены
некоторые наиболее часто используемые
межмолекулярные потенциалы и соответствующие им
функции Майера.
Подставляя определение (2.20) и разложение (2.19) в
определение конфигурационного интеграла (2.8),
находим:
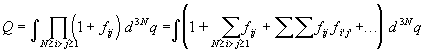 . (2.21) . (2.21)
Скобка под знаком интеграла содержит 2N(N–1)/2
слагаемых, каждое из которых представляет собой
либо функцию Майера для двух конкретных частиц,
либо произведение нескольких (вплоть до N)
таких функций.
До сих пор при расчете конфигурационного
интеграла мы использовали только приближение
парных потенциалов (2.16). Теперь мы введем еще
одно, довольно грубое приближение, которое
справедливо только для сильно разреженных
газов, а именно: в интеграле (2.21) пренебрежем
всеми произведениями функций Майера:
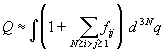 . (2.22) . (2.22)
Таблица 2.1. Наиболее распространенные
межмолекулярные потенциалы
| Название |
Формула |
| Потенциал твердых сфер |
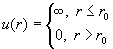 |
| Прямоугольная яма |
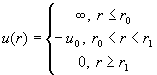 |
Потенциал
Леннард-Джонса |
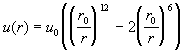 |
Потенциал
Сазерленда |
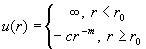 |
exp - 6
потенциал |
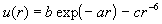 |
Физически это приближение означает следующее.
Мы видели, что функция f(rij) мала,
если расстояние между двумя частицами rij
превышает несколько молекулярных диаметров.
Произведение двух и более функций f(rij)
значительно отличается от 0 только, если
соответствующие частицы i и j находятся
рядом друг с другом. Например, произведение f12
f15f25 f27 соответствует
следующему расположению частиц:
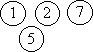
Оставляя в (2.21) только индивидуальные функции
Майера, мы учитываем только те конфигурации, при
которых две частицы находятся рядом, а остальные
удалены друг от друга на значительные
расстояния. Это соответствует состоянию сильно
разреженного газа.
С учетом этого приближения, дальнейшие расчеты
весьма просты. Во-первых, интеграл в (2.22)
разбивается на сумму интегралов. Интеграл от 1 по
координатам всех частиц равен VN. Каждая
функция Майера fij зависит от координат
только двух частиц: i-й и j-й. Интеграл по
координатам оставшихся (N–2) частиц дает
множитель VN–2. В оставшемся интеграле
по 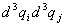 можно перейти к
сферическим координатам. В результате этих
выкладок получим: можно перейти к
сферическим координатам. В результате этих
выкладок получим:
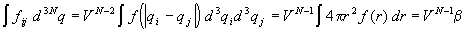
(последний интеграл обозначен буквой  ).Таким образом,
интегралы от индивидуальных функций Майера не
зависят от номеров частиц (i и j). Число
таких интегралов равно числу пар частиц и равно N
(N–1)/2 " N2/2, поэтому
конфигурационный интеграл (2.22) равен ).Таким образом,
интегралы от индивидуальных функций Майера не
зависят от номеров частиц (i и j). Число
таких интегралов равно числу пар частиц и равно N
(N–1)/2 " N2/2, поэтому
конфигурационный интеграл (2.22) равен
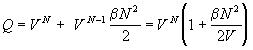 . (2.23) . (2.23)
Мы помним, что все термодинамические функции
зависят от ln Q. При логарифмировании (2.23)
делается предположение о том, что  N 2/2V <<
1: N 2/2V <<
1:
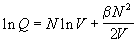 . .
Это предположение ничем не обосновано, однако
оно приводит к правильным результатам.
Дифференцируя логарифм конфигурационного
интеграла по объему, находим уравнение состояния
разреженного газа:
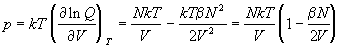 . (2.24) . (2.24)
Из этого уравнения находим второй вириальный
коэффициент:
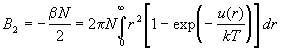 . (2.25) . (2.25)
Это - очень красивая формула, связывающая
макроскопическую физико-химическую величину
(второй вириальный коэффициент) с
микроскопическими параметрами (точнее, с
параметрами межмолекулярного потенциала).
Измеряя зависимость B2 от температуры и
задав функциональную форму межмолекулярного
потенциала, можно определить параметры
потенциала.
В качестве примера рассмотрим газ, в котором
взаимодействие молекул описывается потенциалом
Сазерленда с m = 6 (табл. 2.1). Разобьем область
интегрирования в (2.25) на два интервала: от 0 до r0
и от r0 до Ґ . В первом интервале u(r)
= Ґ , поэтому
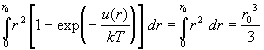 . .
Для расчета интеграла по оставшейся области
предположим, что температура достаточно велика,
а потенциал притяжения мал, так что 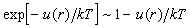 при всех r. Подставляя u(r)
= –с/r6, получим: при всех r. Подставляя u(r)
= –с/r6, получим:
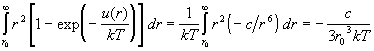 . .
Окончательно, второй вириальный коэффициент
для газа Сазерленда при высоких температурах
равен:
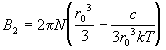 . (2.26) . (2.26)
Если вспомнить, что для газа Ван-дер-Ваальса 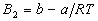 , то можно связать
параметры уравнения состояния a и b с
параметрами потенциала Сазерленда: , то можно связать
параметры уравнения состояния a и b с
параметрами потенциала Сазерленда:
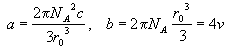 , (2.27) , (2.27)
где 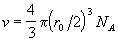 - собственный
объем молекул (радиус молекул равен половине
радиуса действия потенциала: r0/2). Таким
образом, измеряя зависящую и не зависящую от
температуры составляющие второго вириального
коэффициента, можно оценить радиус и объем
молекул, а также силу их притяжения (через
параметры потенциала). - собственный
объем молекул (радиус молекул равен половине
радиуса действия потенциала: r0/2). Таким
образом, измеряя зависящую и не зависящую от
температуры составляющие второго вириального
коэффициента, можно оценить радиус и объем
молекул, а также силу их притяжения (через
параметры потенциала).
2.4.3. Общее выражение для вириальных
коэффициентов
Для того, чтобы получить уравнение состояния
плотных газов, в которых могут образовываться
группы из трех и более молекул, необходимо учесть
все слагаемые в разложении (2.21)
конфигурационного интеграла по функциям Майера.
Эта задача была решена Дж.Майером и
М.Гепперт-Майер с помощью комбинаторных методов.
Мы не будем останавливаться на деталях этих
вычислений, а сразу приведем результаты.
Каждое из 2N(N–1)/2 слагаемых в разложении
(2.21) изображается графической схемой, в которой
каждой функции fij соответствует линия,
соединяющая i-й и j-й кружки. Так, схема
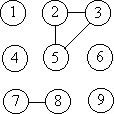
соответствует произведению f23f25f35f78.
В каждой конкретной схеме есть группы молекул,
связанные друг с другом и не связанные с другими
молекулами. Интеграл от такой схемы представляет
собой произведение интегралов по координатам
молекул, входящих в разные группы. Так, например
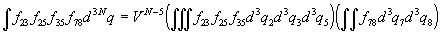 . .
(Интеграл по координатам одиночных молекул, не
связанных с другими молекулами, дал множитель VN–5).
Если интеграл по координатам k молекул,
входящих в группу, нельзя свести к произведению
других интегралов, то такой интеграл называют неприводимым.
Неприводимому интегралу соответствует схема, в
которой от любого кружка отходит не менее двух
линий:
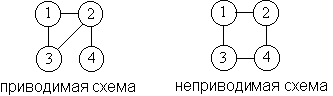
Более строго, k-й неприводимый интеграл  k определяется
следующим образом: k определяется
следующим образом:
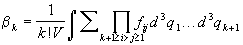 , ,
где сумма берется по всем неприводимым схемам,
содержащим (k+1) частиц. Первые три
неприводимых интеграла имеют вид:
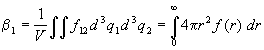 , ,
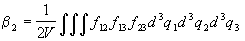 , ,
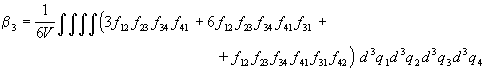 . .
Значения всех неприводимых интегралов не
зависят от номеров частиц, которые используются
в схемах, а определяются только числом
неприводимых схем, соответствующих данному
числу частиц, и качественными характеристиками
схем.
Первому неприводимому интегралу соответствует
простая схема, связывающая две частицы:
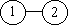 , ,
второму - схема, связывающая три частицы:
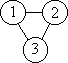 , ,
а третьему - 10 четырехчастичных схем:
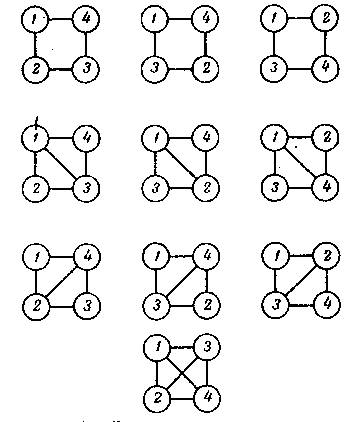
Главный смысл описанных выше неприводимых
интегралов заключается в том, что
конфигурационный интеграл (2.21) выражается через
них в наиболее компактной форме:
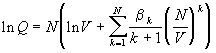 (2.28) (2.28)
Дифференцируя (2.28) по объему, получаем
уравнение состояния в вириальной форме:
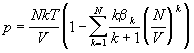 (2.29) (2.29)
Из этого уравнения следует общее выражение для
вириальных коэффициентов:
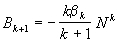 (2.30) (2.30)
Частным случаем этой общей формулы является
формула (2.25) для второго вириального
коэффициента, полученная в приближении сильно
разреженного газа.
Таким образом, статистическая механика
позволяет дать теоретическое обоснование
вириальному разложению и прояснить физический
смысл вириальных коэффициентов. k-й вириальный
коэффициент описывает вклад в давление, который
создают межмолекулярные взаимодействия в
группах из k молекул.
Отметим, что теория реальных газов, изложенная
в данном пункте, перестает работать в области
конденсации. Для этого есть несколько причин,
самая простая из которых связана с тем, что в этой
области несправедливо приближение парного
потенциала (2.16).
|

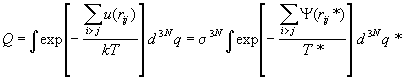 .
.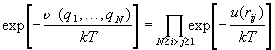 . (2.19)
. (2.19)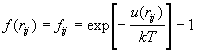 . (2.20)
. (2.20)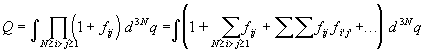 . (2.21)
. (2.21)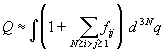 . (2.22)
. (2.22)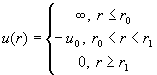
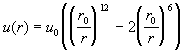
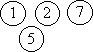
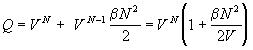 . (2.23)
. (2.23)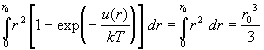 .
.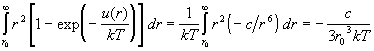 .
.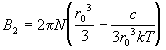 . (2.26)
. (2.26)
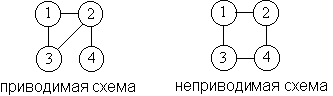
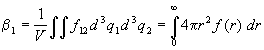 ,
,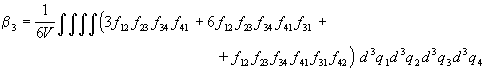 .
. ,
,
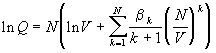 (2.28)
(2.28)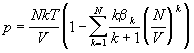 (2.29)
(2.29)